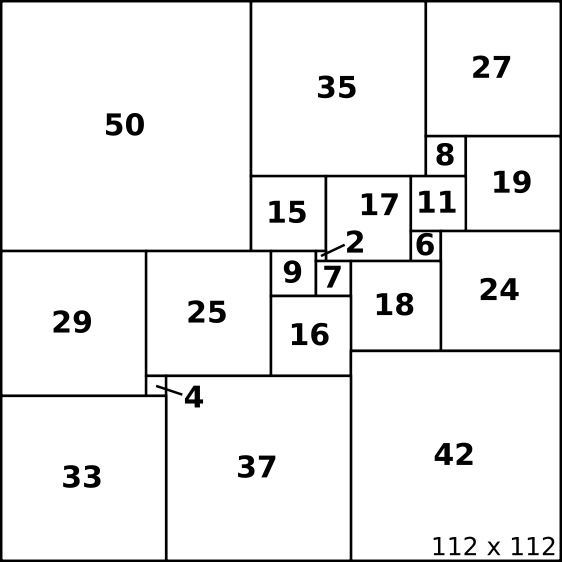
The TMS logo is a squared square—that is, a square partitioned into smaller squares all of different sizes. It is the unique smallest simple squared square (smallest in that it uses the fewest squares, and simple in that no proper subset of the squares of size at least 2 forms a rectangle).
History
The first published examples of squared squares were discovered independently by R. Sprague [3], in 1939, and by four Trinity undergraduates, R.L. Brooks, C.A.B. Smith, A.H. Stone, and W.T. Tutte [1], in 1940. (Brooks and Smith were successive Presidents of the TMS, in 1937 and 1938 respectively.) It was these last four who were the first to study systematically the dissection of squares (and rectangles) into smaller squares. They reinterpreted the problem into one of electrical circuits—faces of a square or rectangle dissection were replaced by resistors in an electrical network, connected at the top and bottom edges of the faces.
The squared square used in the TMS logo (that is, the smallest simple squared square) was discovered in 1978 by an exhaustive computer search [2].
Some excerpts of [1] are available from this site:
An interesting survey article has been written by Tutte [4] on the subject of squared squares, which is now available online.
A Square of Squares
The top of this table shows the solution to the problem of filling a square with other squares; no two squares having the same size. The solution is taken from page 333 of Vol 7 December 1940 Duke Mathematical Journal.
The actual sizes of the squares are 0.7 x the values given in the figure above in mm. The table was made by R.R.G. Rivington in December 1982.
J.F. van Royenweg 5[?]
The Hague
Thus the squared square on the table is the one that appears in [1]; it has side length 608 and comprises 26 squares. (By way of comparison, the TMS logo has side length 112 and comprises 21 squares.)
The design on the table is a graphical incarnation of the (not-so-well-known) identity
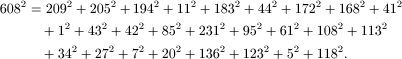
A Glass Square of Squares
Prof. Spiegelhalter, FRS, has rendered a four colouring of a minimal squared square in glass.
[1] Brooks, R.L., Smith, C.A.B., Stone, A.H., and Tutte, W.T., The dissection of rectangles into squares, Duke Math. J. 7 (1940) 312-340.
[2] Duijvestijn, A.J.W., Simple perfect square of lowest order, J. Combin. Theory Ser. B 25 (1978) 240-243.
[3] Sprague, R., Beispiel einer Zerlegung des Quadrats in lauter verschiedene Quadrate, Math. Z. 45 (1939) 607-608.
[4] Tutte, W.T., The quest of the perfect square, Amer. Math. Monthly 72 (1965) 29-35.




